这次我们不谈技巧，尝试来理解一下那些怎么都学不会的线代概念。

根据 2025 年的 NOI 大纲，线性代数作为 OI 中的考点分散在提高和 NOI 级中，其中有：

• 向量与矩阵
• 矩阵初等变换
• 矩阵运算及高斯消元
• 逆矩阵
• 行列式
• 向量空间、线性相关
• 基与线性基

前三者为提高考点，后四者为 NOI 级考点。线性代数相关内容常常作为优化性能或者突破口而出现，如优化递推和线性基在位运算相关题目的运用。我属于那种学了又忘忘了又学每次都好像学会回头就忘的类型，这次把这几个考点串起来写一篇长文，照着 OI Wiki 来写注解和笔记。

在开篇之前感谢 3B1B 系列视频让笔者醍醐灌顶，还有机械工业出版社的《线性代数及其应用》一书，两者都同时囊括了生动和深度，非常值得一看。

向量

$\text{vector}$ 的定义根据学科的不同而有很大的差异，学习过高中物理的同学也都知道，在物理学中有“标量”和“矢量”之称，在 OI 中，由于偏向于 CS 的属性，我们统一将其命名为“向量”，记为 $\vec{v}, \boldsymbol{v}$。

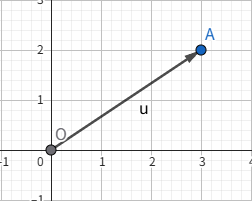
向量作为线性代数中最为基础的部分，在线性代数中通过研究其加法和乘法来探索和思考，向量是一种既有大小又有方向的量，我们同时也可以将其视为一种特定的运动，类似于在数轴上平移，我们在坐标系内以原点为起点画一条有向的线段，例如对于向量 $\begin{bmatrix} 3 \\ 2 \end{bmatrix}$，在几何意义上

就是这样一条从原点开始，沿着 $x$ 轴正方向移动 $3$ 个单位，并沿着 $y$ 轴正方向移动 $2$ 个单位的有向线段。这里有几个概念：

• 向量的模：有向线段 $\vec{u}$ 的长度称为向量的模，即该向量的大小，记作 $|\vec{u}|$
• 单位向量：模为 $1$ 的向量称为该方向上的单位向量，记作 $\vec{e}$

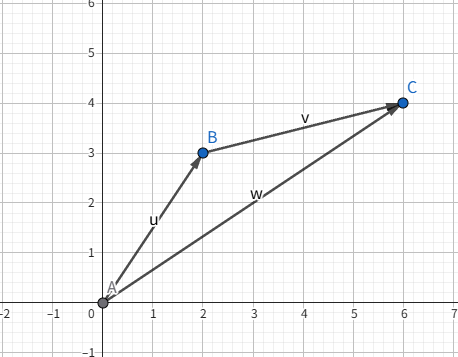
在编写代码中，向量 $\text{vector}$ 实际上就是一种 $\text{array}$：有序的数字列表。类比数的运算，向量加法就是把对应的项相加，或者我们换一种角度，从物理学中的位移概念来看，对于一个人经过的位移 $\overrightarrow{AB} + \overrightarrow{BC}$，我们可以将其看为 $\overrightarrow{AC}$。

线性组合和向量空间

Easy version

有一个重要的观点是：向量的加法和乘法可以看成向量的缩放和相加。据此，我们重新审视点坐标的表示：

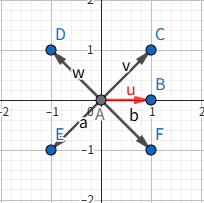
暂不考虑向量空间和基的严谨表述，我们定义如下图的 $\hat{i}, \hat{j}$ 为坐标系的基向量。

当我们将坐标视为标量，实际上任意的标量都是基向量缩放相加相加处理得来的，当我们用数字描述向量时，事实上就依赖于我们的基。不难发现选取不同的基对于“同一位置”的向量有着不同的表示。

$$ a \vec{u} + b \vec{v} = \vec{w}, a, b \in \mathbb{R} $$

这种操作称之为“线性组合”，而这个由所有 $\vec{w}$ 构成的全集，即对于所有可以表示为给定向量线性组合的集合，称之为线性空间、向量空间，更准确地说是向量子空间，如果你看过 3B1B 的视频，译者巧妙地将这个 span 翻译成了“给定向量张成的空间”，非常形象生动。

对于二维向量的向量空间显然有 3 种情况：点、共线、平面。

为了便于研究，在研究单个向量时我们将其视作一条箭头，在有多个向量时，我们则简单地将其视为点，因为正如我们上面所说，在研究时我们将其起点视为原点 $(0, 0)$。

在三维空间的角度下，两个向量的缩放怎样呢？显然我们沿着缩放后的终点绘图可以得到一个过原点的平面，此时我们再施加第三个向量并对其进行缩放，形象地思考，这等同于将前两个向量张开的平面沿着新向量的方向来回移动，从而得到整个空间。

对于若干个向量，如果我们可以通过移除其中的一个向量而不减少向量张成的空间，我们称它们为“线性相关”的向量。这等价于一个向量可以表述为其他向量的线性组合，因为这个向量落在其他向量张开的空间里，无法形成新的约束。

若这若干个向量都给向量空间增加了新的维度，则它们是“线性无关”的。

更进一步的 Hard version

来看看严谨的定义如何吧。

一个向量空间是由一些被称为向量的对象构成的非空集合 $V$，在这个集合上定义了两个运算，称之为加法和标量乘法（标量属于全体实数），对于 $V$ 中所有向量 $u, v, w$ 及所有的标量 $c, d$ 都要服从以下公理：

1. $\vec{u} + \vec{v} \in V$
2. $\vec{u} + \vec{v} = \vec{v} + \vec{u}$
3. $(\vec{u} + \vec{v}) + \vec{w} = \vec{u} + (\vec{v} + \vec{w})$
4. $V$ 中存在一个零向量 $0$ 使得 $\vec{u} + 0 = \vec{u}$
5. 对 $V$ 中每个向量 $\vec{u}$，存在一个向量 $-\vec{u}$ 使得 $\vec{u} + (-\vec{u}) = 0$
6. $c \vec{u} \in {V}$
7. $c(\vec{u} + \vec{v}) = c\vec{u} + c\vec{v}$
8. $(c + d)\vec{u} = c\vec{u} + d\vec{v}$
9. $c(d\vec{u}) = c(d\vec{u})$
10. $1\vec{u} = \vec{u}$

称向量空间 $V$ 的一个极大线性无关向量集为 $V$ 的一组线性基，简称基。在 OI 中一般而言只会考虑 $n$ 维实线性空间 $\mathbf{R}^n$ 和 $n$ 维布尔域线性空间 $\mathbf{Z}_{2}^{n}$。

如果你对于线性空间与群的关系感兴趣，或者说愿意阅读更多严谨的表述，可以参见 线性空间 - OI Wiki，虽然我觉得不是非常好懂。

矩阵与线性变换

在线性代数中，向量有列向量和行向量之分，主要研究列向量。对于一个矩阵 $A$，主对角线指的是 $A_{i, i}$ 上的元素，定义单位矩阵 $I$ 表示主对角线上为 $1$，其余均为 $0$。

$\text{linear transformation}$ 中的 transformation 一词其实就是 $\text{function}$ 的意味，而 transformation 寓意着这一关系可以通过某种特定的方式来可视化，定义线性变换为：

1. 所有直线在变换后仍然保持直线，不能有所弯曲，更进一步，所有“网格线”在线性变化之后仍应该保持平行且等距分布
2. 原点保持固定

实际上，由于线性代数研究中对于线性变化的约束，对于任意一个向量在线性变化后的坐标，只需要通过记录基向量 $\hat{i}, \hat{j}$ 变化后的位置。还记得这个式子吗？

$$ \begin{aligned}& a \vec{u} + b \vec{v} = \vec{w}, a, b \in \mathbb{R} \ & \vec{v} = a \hat{i} + b \hat{j} \end{aligned} $$

在变换之后仍然有：

$$ \vec{v}’ = a \hat{i}’ + b \hat{j}' $$

获取基向量 $\hat{i}, \hat{j}$ 的信息只需要四个数字：变换后的 $x_{\hat{i}}, y_{\hat{i}}, x_{\hat{j}}, y_{\hat{j}}$。

把这四个元素丢在一个矩阵里，有一个专有名称称之为 $2 \times 2$ 矩阵（$\text{Two-by-Two Matrix}$）：

$$ \begin{bmatrix} x_{\hat{i}} & x_{\hat{j}} \\ y_{\hat{i}} & y_{\hat{j}} \end{bmatrix} $$

这也就是为什么在线性代数中研究对象通常为列向量。矩阵作为一个载体，记录着一个线性变化的信息，还记得我们对于坐标的标量表示吗？现在我们可以推出矩阵乘向量的表达了：

$$ \begin{bmatrix} a & b \\ c & d \end{bmatrix} \times \begin{bmatrix} x \\ y \end{bmatrix} = x \begin{bmatrix} a \\ c \end{bmatrix} + y \begin{bmatrix} b \\ d \end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy \end{bmatrix} $$

有一种特殊的矩阵形如：

$$ \begin{bmatrix} 1 & a \\ 0 & b \end{bmatrix} $$

这种变换中，$\hat{i}$ 不发生变化，它有一个特殊的名字为“剪切”（$\text{shear}$）：

如果变换后的 $\hat{i}, \hat{j}$ 是线性相关的，意味着其中一个向量是另一个向量的某种缩放（倍数关系），这个线性变换将整个二维平面积压在该向量组所在的直线上。

正如我们上文所说，从动态的视角来看，矩阵是对某空间的一种特定变换。

矩阵有一种特殊的操作称之为“转置”：在其右上角写上转置 $^{\boldsymbol{T}}$，表示交换矩阵的行与列。

矩阵乘法

由上文，线性变换完全取决于对空间内基向量的作用情况，当我们将矩阵和向量相乘时，就是将矩阵所描述的变换作用在向量上。现在我们来看看如何实现一个包含了“旋转”和“剪切”的复合变换：

$$ \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}, \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} $$

这两个矩阵分别对平面内向量进行 shear 和 rotate 操作，两个矩阵相乘有几何意义：两个线性变化相继作用：

$$ \overleftarrow{\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}, \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}} $$

值得注意的是，矩阵乘法从右往左读，为什么？如果我们将矩阵变化看作一个函数，则对于向量 $\vec{v}$ 的作用有：

$$ f(g(\vec{v})) $$

对于函数的复合，显然是从内往外读，这样理解就自然的多。

对于两个矩阵中的不同列，我们分别视为元素和变化，抽离出来有：

$$ \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} e & f \\ g & h \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \times \begin{bmatrix} e \\ g \end{bmatrix} + \begin{bmatrix} a & b \\ c & d \end{bmatrix} \times \begin{bmatrix} f \\ h \end{bmatrix} = \begin{bmatrix} a \times e + b \times g & a \times f + b \times h \\ c \times e + d \times g & c \times f + d \times h \end{bmatrix} $$

注意到，矩阵乘法不具有交换律，从几何意义来看显然，举个例子，先旋转再剪切显然不一定等于先剪切再旋转。但是矩阵乘法具有分配律，也就是说：

$$ \boldsymbol{(AB)C} = \boldsymbol{A(BC)} $$

当然可以继续从几何的层面来思考这个问题，但是我们换个角度，如果拆开来看，将 $\boldsymbol{AB}$ 视为一个整体，那么无论如何加上括号操作，操作顺序永远是：$\boldsymbol{C} \to \boldsymbol{B} \to \boldsymbol{A}$。这样我们就轻松证明出了矩阵乘法重要的性质之一。

$3 \times 3$ 的矩阵乘法同理，这里不再赘述：

$$ \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = x \begin{bmatrix} a \\ d \\ g \end{bmatrix} + y \begin{bmatrix} b \\ e \\ h \end{bmatrix} + z \begin{bmatrix} c \\ f \\ i \end{bmatrix} $$

行列式

在线性变换中，将坐标新中基向量张开的小正方形面积改变的比例称之为其行列式，记为 $\det(\boldsymbol{A})$。

如果一个二维线性变换的 $\det = 0$，则说明其将整个空间压缩在了一条线，或者说一个点上。一言概之，如果我们想要知道这个矩阵代表的变换下是否压缩了空间的维度，只需要检验其 $\det$ 是否为 $0$ 即可。

但是行列式是可以为负的？如何解释负的 $\det$ 呢？面积的比例显然不可能为负。

注意到，将行列式套上绝对值，其仍然表示面积缩放的比例，负号类比物理运动学，代表方向：标志着空间中的定向发生了变化，换而言之，基向量之间的相对位置发生了改变。三维下：

具体的有右手定则来判断三维空间中定向的改变。

逆矩阵，列空间，零空间

逆矩阵 $\boldsymbol{A}^{-1}$ 称为矩阵 $\boldsymbol{A}$ 的逆矩阵当且仅当 $\boldsymbol{AA}^{-1} = \boldsymbol{I}$，或者说，

矩阵的引入来自于线性方程组。将线性方程组的系数抽出来，写成矩阵乘法的形式更为方便，而逆矩阵的存在使得我们能够求解方程组，具体的：

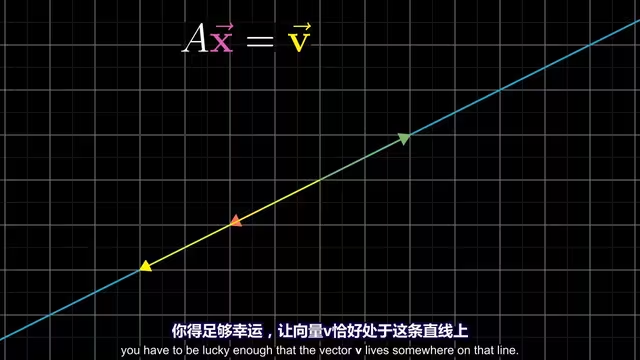
$$ \boldsymbol{AA}^{-1} \vec{x} = \boldsymbol{A}^{-1} \vec{v} $$

当 $\det(\boldsymbol{A}) \neq 0$ 时 $\boldsymbol{A}^{-1}$ 存在，可以使用高斯消元求解。

注意到即使不存在逆矩阵，方程仍然可能存在解。就是这种清况：

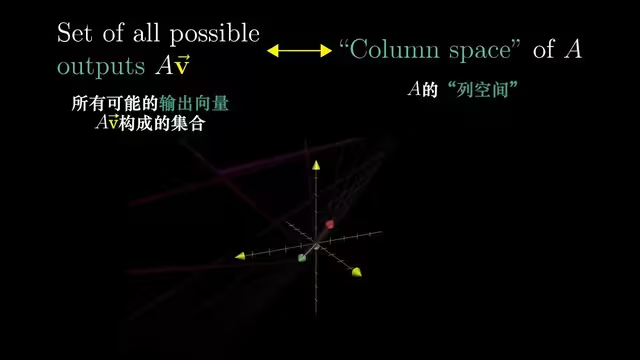
这里我们引出秩的概念：当变换的结果为一条直线时（一维），我们称这个变换的秩为 $1$。如果变换后的向量落在某个二维平面上，我们称这个变换的秩为 $2$。秩代表着变换后空间的维度。

列空间是矩阵的列所张开的空间，秩其实是列空间的维数。

有一种特殊的秩：满秩。在这种情况下，秩与列数相等。

由于线性变换的要求之一是保持原点位置不变，所以零向量一定会包含在列空间中。对于满秩变换：只有零向量会在变换后落在原位置；但如果矩阵非满秩，则会压缩最终空间的维度，这意味着会有一部分向量被变换成了零向量。

变换后落在原点的向量集合被称之为“零空间”或者核（Kernel）。

• 当逆矩阵存在时，我们可以用其求解方程组
• 列空间让我们得知何时存在解
• 零空间有助于体现所有可能的解的集合